در این مقاله از وبسایت اسدیتا، در خصوص ضریب همبستگی چیست؟ چگونه در تحلیل دادهها مورد استفاده قرار میگیرد؟ بحث خواهیم کرد.
ضریب همبستگی یا correlation coefficient یک معیار آماری است که نشان میدهد چقدر دو متغیر با یکدیگر همبستگی دارند.
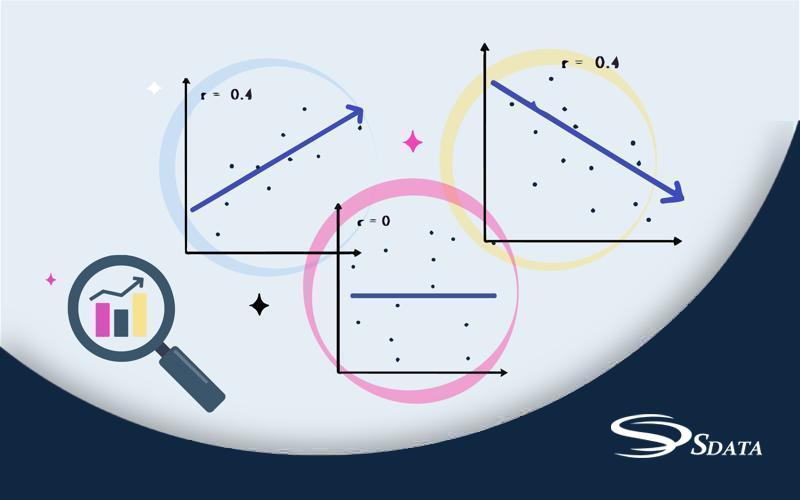
به عبارت دیگر، این معیار نشان میدهد که دو متغیر در چه میزان با یکدیگر مرتبط هستند. ضریب همبستگی بین دو متغیر از -1 تا 1 متغیر است.
اگر ضریب همبستگی بین دو متغیر برابر با 1 باشد، این نشانگر همبستگی مثبت کامل بین دو متغیر است، به عبارت دیگر، هر افزایش یک واحد در مقدار یک متغیر، باعث افزایش مقدار دیگری نیز به اندازهی یک واحد میشود.
اگر ضریب همبستگی برابر با 0 باشد، در این صورت دو متغیر با هم هیچ رابطهای ندارند.
در صورتی که ضریب همبستگی بین دو متغیر برابر با -1 باشد، این نشانگر همبستگی منفی کامل بین دو متغیر است، به عبارت دیگر، هر افزایش یک واحد در مقدار یک متغیر، باعث کاهش مقدار دیگری نیز به اندازهی یک واحد میشود.
کاربرد ضریب همبستگی چیست؟
ضریب همبستگی در تحلیل دادهها بسیار مفید است، به عنوان مثال اگر بخواهیم بررسی کنیم که دو متغیر چه میزان با یکدیگر مرتبط هستند، میتوانیم از ضریب همبستگی استفاده کنیم.
ضریب همبستگی به عنوان یک ابزار مفید برای پیشبینی مقادیر یک متغیر بر اساس مقدار دیگری نیز مورد استفاده قرار میگیرد.
ضریب همبستگی در تحلیل دادههای دو متغیره مورد استفاده قرار میگیرد، اما برای تحلیل دادههای چند متغیره، میتوان از ضریب همبستگی ماتریسی استفاده کرد، که نشاندهندهی همبستگی بین هر دو متغیر در دستهی متغیرهاست.
در نهایت، باید توجه داشت که ضریب همبستگی تنها یکی از ابزارهای مورد استفاده در تحلیل دادهها است و برای بهترین تحلیل داده، باید از چندین ابزار و تکنیک آماری استفاده کرد.
آیا ضریب همبستگی برای تحلیل دادههای چند متغیره نیز مورد استفاده قرار میگیرد؟
برای بررسی اینکه ضریب همبستگی چیست؟ چگونه در تحلیل دادهها مورد استفاده قرار میگیرد، باید بدانیم که این عامل در دادههای چند متغیره نیز استفاده میشود یا خیر.
ضریب همبستگی برای تحلیل دادههای چند متغیره نیز مورد استفاده قرار میگیرد. در واقع، ضریب همبستگی بین دو متغیر در تحلیل دادههای دو متغیره فقط یک حالت خاص از ضریب همبستگی بین چند متغیر است.
برای تحلیل دادههای چند متغیره، ضریب همبستگی ماتریسی (correlation matrix) معرفی میشود که نشان دهندهی همبستگی بین هر دو متغیر در دستهی متغیرهاست.
در ضریب همبستگی ماتریسی، هر ستون و سطر متناظر با یک متغیر است و مقادیر ضریب همبستگی بین دو متغیر در سلول متناظر با آنها در ماتریس قرار میگیرد.
ضریب همبستگی ماتریسی میتواند به عنوان یک ابزار مفید در تحلیل دادههای چند متغیره مورد استفاده قرار گیرد، به عنوان مثال برای بررسی رابطه بین چندین متغیر و یافتن متغیرهایی که با هم همبستگی بالایی دارند، یا برای پیشبینی مقادیر یک متغیر بر اساس مقادیر دیگری در دستهی متغیرها.
در کل، ضریب همبستگی به عنوان یکی از ابزارهای مهم در تحلیل دادهها برای بررسی رابطه بین متغیرها و پیشبینی مقادیر آینده مورد استفاده قرار میگیرد، و میتواند در تحلیل دادههای دو متغیره و چند متغیره مورد استفاده قرار گیرد.
ضریب همبستگی ماتریسی برای تحلیل دادههای چند متغیره در چه مواردی مفید است؟
ضریب همبستگی ماتریسی به عنوان یکی از ابزارهای مهم در تحلیل دادههای چند متغیره میتواند در موارد زیر مفید باشد:
بررسی رابطه بین چندین متغیر:
با استفاده از ضریب همبستگی ماتریسی، میتوانیم رابطه بین چندین متغیر را بررسی کنیم و به دنبال متغیرهایی با همبستگی بالا باشیم. این متغیرها میتوانند به عنوان ورودیهای مدلهای پیشبینی و تحلیل پارامتری مورد استفاده قرار بگیرند.
پیشبینی مقادیر متغیرها:
با استفاده از ضریب همبستگی ماتریسی، میتوانیم مقادیر یک متغیر را بر اساس مقادیر دیگری در دستهی متغیرها پیشبینی کنیم.
به عنوان مثال، اگر ضریب همبستگی بین درآمد و مصرف برق در یک شهر بالا باشد، میتوانیم بر اساس مقدار درآمد، میزان مصرف برق را پیشبینی کنیم.
تحلیل علل و معلولیت:
با استفاده از ضریب همبستگی ماتریسی، میتوانیم رابطه بین متغیرها را بررسی کنیم و به دنبال علل و معلولیت در میان آنها باشیم.
به عنوان مثال، اگر ضریب همبستگی بین دما و میزان فروش یک کالا،بالا باشد، میتوانیم بر اساس تحلیل دادهها، بفهمیم که آیا دما علت اصلی افزایش فروش است یا اینکه دلایل دیگری هم در پشت این رابطه وجود دارد.
ضریب همبستگی ماتریسی به عنوان یکی از ابزارهای مهم در تحلیل دادههای چند متغیره که به دنبال رابطه بین متغیرها و پیشبینی مقادیر آینده هستیم، مورد استفاده قرار میگیرد.
نحوهی محاسبهی ضریب همبستگی ماتریسی
برای درک بهتر اینکه ضریب همبستگی چیست؟ چگونه در تحلیل دادهها مورد استفاده قرار میگیرد، باید نحوه محاسبه ضریب همبستگی را محاسبه کنیم. ضریب همبستگی ماتریسی برای دو متغیر به شکل زیر محاسبه میشود:
r_{xy} = \frac{cov(x,y)}{\sigma_x \sigma_y}
در این فرمول، r_{xy} ضریب همبستگی بین دو متغیر x و y است، cov(x,y) ماتریس کوواریانس بین x و y است، و \sigma_x و \sigma_y انحراف معیار متغیرهای x و y هستند.
برای محاسبه ضریب همبستگی ماتریسی بین چندین متغیر، میتوان برای هر دو متغیر یک ماتریس کوواریانس محاسبه کرد و سپس با تقسیم هر مقدار در ماتریس کوواریانس بر حاصلضرب انحراف معیار متغیرهای مربوطه، ضریب همبستگی بین آن دو متغیر را به دست آورد.
در نهایت، یک ماتریس ضریب همبستگی ماتریسی به دست میآید که در آن هر سطر و ستون نشاندهندهی یک متغیر است و مقادیر در سلولهای متناظر نشاندهندهی ضریب همبستگی بین دو متغیر است. ضریب همبستگی ماتریسی در بازهی [-1, 1] قرار دارد.
ضریب همبستگی ماتریسی برابر با 1 نشاندهندهی همبستگی مثبت کامل بین دو متغیر است، در حالی که ضریب همبستگی ماتریسی برابر با -1 نشاندهندهی همبستگی منفی کامل بین دو متغیر است.
ضریب همبستگی ماتریسی برابر با 0 نشاندهندهی رابطهای بین دو متغیر نیست، به عبارت دیگر، دو متغیر مستقل هستند. همچنین، هر چه ضریب همبستگی ماتریسی به سمت ۱ یا -۱ نزدیکتر باشد، همبستگی بین دو متغیر بیشتر است و هر چه به سمت صفر نزدیکتر باشد، همبستگی بین دو متغیر کمتر است.
آیا ضریب همبستگی ماتریسی همیشه نشاندهندهی رابطهی علّی بین دو متغیر است؟
خیر، ضریب همبستگی ماتریسی همیشه نشاندهندهی رابطهی علّی بین دو متغیر نیست.
ضریب همبستگی ماتریسی تنها نشاندهندهی میزان همبستگی و ارتباط بین دو متغیر است و این ارتباط ممکن است به صورت علّی، غیرعلّی و یا تصادفی باشد.
در واقع، وجود همبستگی بین دو متغیر نشان میدهد که تغییرات در یکی از متغیرها ممکن است باعث تغییراتی در متغیر دیگر نیز شود، اما این نشاندهندهی رابطهی علّی نیست و ممکن است به صورت تصادفی و یا با وجود علّیتی دیگری بین دو متغیر رخ دهد.
برای تشخیص رابطهی علّی بین دو متغیر، نیاز است که به عوامل دیگری که ممکن است تأثیر گذار باشند بر تغییرات دو متغیر، اهمیت داده شود و از روشهای مختلف تحلیل داده برای تحلیل رابطهی علّی استفاده شود.
به عنوان مثال، در یک مطالعهی علّی، باید مطمئن شد که تغییرات در یک متغیر به دلیل تغییرات در متغیر دیگر رخ داده است و نه به دلیل عوامل دیگری مانند اختلافات ناشی از تفاوت در ویژگیهای افراد یا شرایط مختلفی که در دو گروه متفاوت اعمال شده است.
سخن پایانی
در این مقاله با توضیح اینکه ضریب همبستگی چیست؟ چگونه در تحلیل دادهها مورد استفاده قرار میگیرد، بحث شد.
به شکل کلی برای درک بهتر ضریب همبستگی باید به منابع گستردهتری دسترسی پیدا کنید. برای اطلاعات بیشتر در این زمینه نیز میتوانید به وبسایت اسدیتا مراجعه کنید.
کلمات مرتبط
- correlation coefficient چیست
- ضریب تعیین r2
- ضریب همبستگی
- ضریب همبستگی چیست