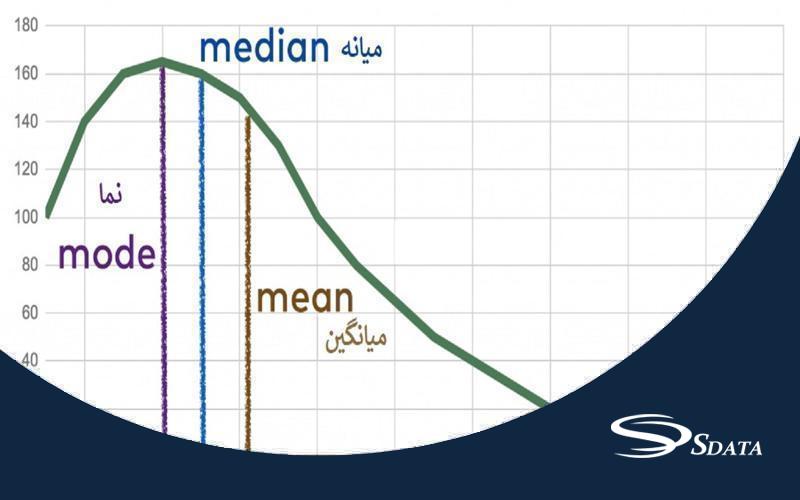
در آمار، مفاهیم میانگین، میانه و مد به عنوان معیارهای مختلفی برای بیان میزان مرکزیت داده‌ها در نظر گرفته می‌شوند.

در این مقاله از وبسایت اس‌دیتا، به بررسی تفاوت بین میانگین، میانه و مد در آمار و کاربردهای هرکدام پرداخته خواهد شد. این سه مورد به تنهایی می‌توانند از اصول و مفاهیم مهم و پایه در علم آمار باشند.

بررسی  میانگین، میانه و مد در آمار

در این بخش به توضیح و بررسی هر کدام از این موارد می‌پردازیم.

میانگین:

میانگین یا میانه ریاضی، مجموع تمام اعداد در یک مجموعه را تقسیم بر تعداد اعداد موجود در آن مجموعه می‌دهد. به عبارت دیگر، میانگین میزان مرکزیت داده‌ها را به عنوان میانگین در نظر می‌گیرد.

میانگین برای داده‌هایی که توزیع آن‌ها نزدیک به یکنواخت است و همچنین برای داده‌هایی که بدون توجه به مقدار مثبت یا منفی هستند مفید است.

برای مثال، میانگین می‌تواند برای محاسبه‌ی متوسط درآمد، میانگین دمای یک منطقه، میانگین تعداد کلیک‌ها در یک وبسایت و موارد مشابه به کار رود.

میانه:

میانه، مقدار وسطی یک مجموعه از اعداد است. به عبارت دیگر، از داده‌ها، مقداری که در وسط مجموعه قرار دارد، به عنوان میانه در نظر گرفته می‌شود.

میانه برای داده‌هایی که توزیع آن‌ها به شدت از نرمال فاصله دارد و گاهی اوقات برای داده‌هایی که دارای پرتی هستند مفید است. برای مثال، میانه می‌تواند برای محاسبه‌ی میزان سن، میانه‌ی امتیازات در یک مسابقه و موارد مشابه به کار رود.

مد:

مد، مقداری است که در فراوانی بیشترین تکرار دارد. به عبارت دیگر، مد نشان‌دهنده‌ی مقداری است که بیشترین تعداد بار تکرار شده است.

مد برای داده‌هایی که دارای توزیع غیرنرمال هستند و همچنین برای داده‌هایی که دارای دو یا چند پیک هستند، مفید است. برای مثال، مد می‌تواند برای محاسبه‌ی میزان ترافیک در یک راه‌آهن، میزان پرداخت در یک مسابقه و موارد مشابه به کار رود.

تفاوت بین این سه مفهوم در این است که هر یک به صورت مختلفی میانگین داده‌ها را محاسبه می‌کند.

میانگین به صورت مجموع مقادیر داده‌ها تقسیم بر تعداد داده‌ها است، میانه به عنوان مقدار وسطی داده‌ها تعریف می‌شود و مد به عنوان مقداری که بیشترین تعداد بار تکرار شده است، تعریف می‌شود.

در کاربردهای مختلف، هر یک از این سه مفهوم مفید است. انتخاب مفهوم مناسب برای محاسبه‌ی میانگین داده‌ها، به دلیل توزیع داده‌ها، مهم است.

برای مثال، در داده‌هایی که دارای توزیع غیرنرمال هستند، میانگین ممکن است از میانه یا مد مناسب‌تر باشد.

همچنین، در داده‌هایی که دارای پرتی هستند، میانگین ممکن است از میانه مناسب‌تر باشد. میانگین، میانه و مد به عنوان معیارهای مختلفی برای بیان میزان مرکزیت داده‌ها استفاده می‌شوند.

هر یک از این معیارها برای محاسبه‌ی میانگین داده‌ها در شرایط خاصی مفید است و باید با توجه به توزیع داده‌ها و شرایط مختلف، مورد استفاده قرار گیرد.

ویژگیهای میانگین، میانه و مد در آمار

در آمار، میانگین، میانه و مد سه شاخص اصلی برای توصیف ویژگی‌های داده‌ها هستند و هرکدام کاربرد خاص خود را دارند. این تفاوت‌ها به شما کمک می‌کنند تا درک بهتری از ویژگی‌های یک مجموعه داده پیدا کنید.

1. میانگین (Mean)

• تعریف: میانگین مجموع تمامی مقادیر داده‌ها را تقسیم بر تعداد داده‌ها است. به عبارت دیگر، میانگین از فرمول زیر به‌دست می‌آید:

  میانگین=∑xin\text{میانگین} = \frac{\sum x_i}{n}

  که در آن xix_i مقادیر داده‌ها و nn تعداد داده‌ها هستند.

• ویژگی‌ها:

  • میانگین به مقادیر افراطی (آوتلایرها) حساس است. اگر داده‌ها شامل مقادیر بسیار بزرگ یا کوچک باشند، میانگین می‌تواند به‌طور قابل‌توجهی تغییر کند.
  • میانگین برای داده‌های توزیع‌شده به‌طور یکنواخت و نرمال مفید است.

• کاربردها:
  میانگین معمولاً در تحلیل‌های اقتصادی، مالی، و علمی برای ارائه یک تصویر کلی از داده‌ها استفاده می‌شود. برای مثال، برای محاسبه میانگین درآمد در یک گروه یا میانگین نمرات یک آزمون.

2. میانه (Median)

• تعریف: میانه مقداری است که داده‌ها را به دو قسمت مساوی تقسیم می‌کند. برای محاسبه میانه، ابتدا داده‌ها را به ترتیب صعودی یا نزولی مرتب کرده و مقدار وسطی را انتخاب می‌کنیم. اگر تعداد داده‌ها فرد باشد، میانه مقدار وسطی است؛ اگر تعداد داده‌ها زوج باشد، میانه میانگین دو مقدار وسطی است.

• ویژگی‌ها:

  • میانه نسبت به آوتلایرها مقاوم است. به این معنا که اگر داده‌ها شامل مقادیر افراطی باشند، میانه تغییرات زیادی نمی‌کند.
  • میانه معمولاً در توزیع‌های نامتقارن یا زمانی که داده‌ها از لحاظ توزیع نرمال نیستند، استفاده می‌شود.

• کاربردها:
  میانه در تحلیل‌های اقتصادی و اجتماعی مفید است، به‌ویژه زمانی که توزیع داده‌ها نرمال نباشد. مثلاً در تحلیل درآمد خانواده‌ها در یک کشور، ممکن است از میانه برای اجتناب از تأثیرات زیاد درآمدهای بسیار بالا یا پایین استفاده شود.

3. مد (Mode)

• تعریف: مد به مقدار یا مقادیری از داده‌ها گفته می‌شود که بیشترین فراوانی را دارند. داده‌ها ممکن است یک مد، چند مد یا هیچ مدی نداشته باشند.

• ویژگی‌ها:

  • مد به‌ویژه زمانی که داده‌ها تکرار زیادی دارند، مفید است.
  • در برخی از داده‌ها ممکن است هیچ مدی وجود نداشته باشد یا بیشتر از یک مد (در مواردی که بیش از یک مقدار دارای بیشترین فراوانی باشند) وجود داشته باشد.

• کاربردها:
  مد در تحلیل‌های بازاریابی و مصرفی کاربرد دارد. مثلاً برای شناسایی پرطرفدارترین محصولات یا خدمات. همچنین در بررسی ویژگی‌های جمعیتی یا مصرفی، مد می‌تواند مفید باشد.

جمع‌بندی تفاوت‌ها

• میانگین: بهترین برای داده‌های متوازن و بدون آوتلایر است. حساس به داده‌های پرت است.
• میانه: مناسب برای داده‌های نامتقارن یا زمانی که داده‌ها دارای آوتلایر هستند. نسبت به داده‌های خارج از محدوده مقاوم است.
• مد: به‌خصوص زمانی که قصد دارید پرکاربردترین یا رایج‌ترین مقدار را شناسایی کنید، مانند شناسایی محبوب‌ترین محصولات یا ویژگی‌های خاص.

این تفاوت‌ها به انتخاب صحیح معیار مرکزی کمک می‌کنند و به تحلیل‌گران این امکان را می‌دهند که تصویر دقیقی از داده‌ها بدست آورند.

میانگین، میانه و مد در چه شرایطی مفید نیستند؟

در بررسی تفاوت بین میانگین، میانه و مد در آمار و کاربردهای هرکدام استفاده از میانگین، میانه و مد برای بیان میزان مرکزیت داده‌ها در بسیاری از شرایط مفید است، اما در بعضی شرایط ممکن است به عنوان یک معیار مناسب برای بیان میزان مرکزیت داده‌ها نباشند.

در زیر به برخی از شرایطی که در آن استفاده از میانگین، میانه و مد مفید نیست، اشاره می‌کنیم:

داده‌های پرت:

در داده‌هایی که دارای پرتی هستند، میانگین به عنوان معیاری برای بیان میزان مرکزیت داده‌ها مناسب نیست.

به عنوان مثال، اگر در یک داده‌سری، یک داده بسیار بزرگتر یا کوچکتر از سایر داده‌ها وجود داشته باشد، میانگین به شدت تحت تأثیر قرار می‌گیرد. در چنین شرایطی، میانه به عنوان یک معیار مرکزیت مفیدتر است.

داده‌های توزیع غیرنرمال:

در داده‌هایی که توزیع آن‌ها به شدت از توزیع نرمال فاصله دارد، میانگین به عنوان یک معیار مرکزیت مناسب نخواهد بود. به عنوان مثال، اگر داده‌ها به شدت تمرکز شده باشند ولی تعدادی از آن‌ها از بافت داده‌های اصلی خارج شده باشند، میانگین به شدت تحت تأثیر قرار می‌گیرد و ممکن است به عنوان یک معیار نامناسب شناخته شود.

در چنین شرایطی، میانه به عنوان یک معیار مرکزیت مفیدتر است.

داده‌های نامتقارن:

در بعضی داده‌ها، توزیع آن‌ها نامتقارن است و در چنین شرایطی، استفاده از میانگین به عنوان معیار مرکزیت نامطلوب است.

به عنوان مثال، در داده‌هایی که توزیع آن‌ها به شدت از توزیع نرمال فاصله دارد ولی از بافت داده‌های منفی، بسیار کمتری نسبت به بافت داده‌های مثبت دارد، استفاده از میانگین به عنوان معیار مرکزیت مناسب نخواهد بود. در چنین شرایطی، ممکن است مد به عنوان یک معیار مرکزیت مناسب‌تر باشد.

در کل، باید به توزیع داده‌ها و شرایط مختلف توجه کرده و معیار مناسب برای بیان میزان مرکزیت داده‌ها را انتخاب کرد. استفاده از معیار مناسب می‌تواند به دقت و کیفیت تحلیل داده‌ها کمک کند.

چه معیاری برای داده‌های پرت مناسب است؟

در بررسی تفاوت بین میانگین، میانه و مد در آمار و کاربردهای هرکدام بهتر است تا بدانیم چه معاری برای داده‌های پرت مناسب است.

برای داده‌های پرت، معیارهای مرکزیت دیگری به جز میانگین مانند میانه و مد می‌توانند مناسب باشند. در صورتی که داده‌های پرت به شدت تحت تأثیر قرار گرفته باشند، ممکن است میانه به عنوان معیار مناسب‌تر از میانگین باشد. همچنین، استفاده از معیارهای پرت‌تر مانند کوارتیل‌ها و محدوده‌های میانه می‌تواند برای برخی داده‌های پرت مناسب باشد.

یکی از معیارهایی که برای داده‌های پرت مفید است، میانه مطلق است. در این روش، ابتدا میانگین را با استفاده از تمام داده‌ها محاسبه کرده و سپس از این میانگین مطلق، فاصله‌ی داده‌ها با میانگین را محاسبه می‌شود.

میانه مطلق، میانه‌ی این فاصله‌ها است و برای داده‌های پرت مناسب است. همچنین، استفاده از میانه‌ی محدوده برش (trimmed median) نیز برای داده‌های پرت مفید است.

در این روش، بعضی از داده‌های پرت از بین می‌رودند و سپس میانه‌ی داده‌های باقیمانده به عنوان معیار مرکزیت در نظر گرفته می‌شود.

در کل، برای داده‌های پرت، استفاده از میانگین به تنهایی به عنوان معیار مناسب برای بیان میزان مرکزیت داده‌ها مناسب نیست و باید به معیارهای دیگر نیز توجه کرد.

سخن پایانی

• میانگین برای داده‌های متوازن و بدون آوتلایر مفید است.
• میانه زمانی که داده‌ها نرمال نباشند یا آوتلایر وجود داشته باشد، کاربرد دارد.
• مد زمانی که نیاز به شناسایی مقدار رایج یا پرکاربردترین مقدار در داده‌ها باشد، کاربرد دارد.

در این مقاله به موضوع تفاوت بین میانگین، میانه و مد در آمار و کاربردهای هرکدام پرداخته شد. برای اطلاعات بیشتر در خصوص این موارد می‌توانید به وبسایت اس‌دیتا مراجعه نمایید.